Suppose you have the following system to solve:
\[ \begin{cases} 3x + 4y - 5z = -3.5 \\ x - y + z = 1.5 \\ x - 3y + 6z = 16 \end{cases} \]
All the equations must be in the form \(a \cdot x + b \cdot y + c \cdot z = d\).
 , select Algebra > Solve System of Equations > Solve System of Linear Equation.
, select Algebra > Solve System of Equations > Solve System of Linear Equation.
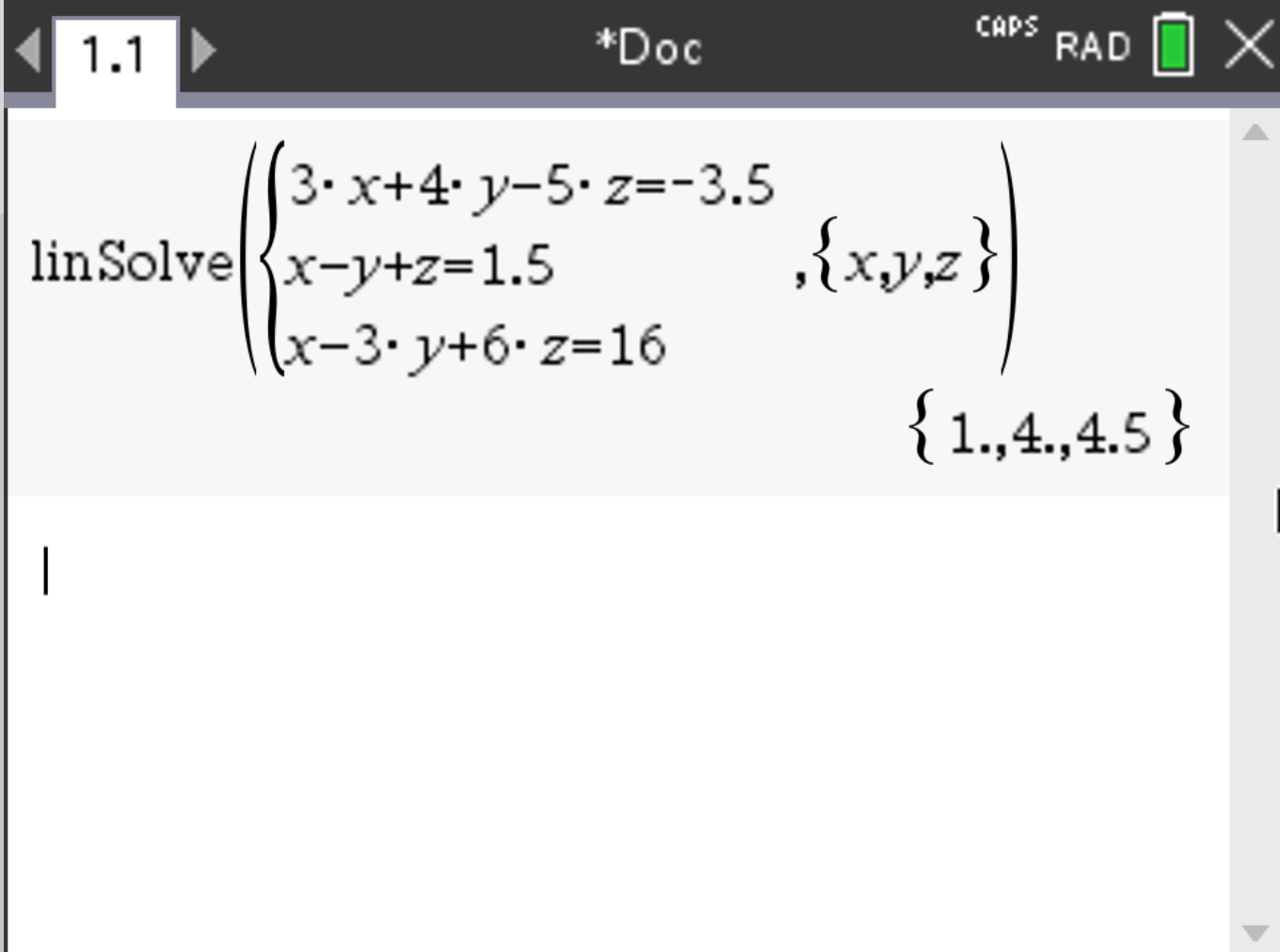
Press  . The results should be \(x = 1\), \(y = 4\), and \(z = 4.5\).
. The results should be \(x = 1\), \(y = 4\), and \(z = 4.5\).
Suppose you have to solve the equation \(x^3 - 10x^2 + 33x - 36 = 0\).
The right-hand side must be 0.
 , select Algebra > Polynomial Tools > Find Roots of Polynomial. Set 3 as the order
of the equation. Fill the equation as follows:
, select Algebra > Polynomial Tools > Find Roots of Polynomial. Set 3 as the order
of the equation. Fill the equation as follows:
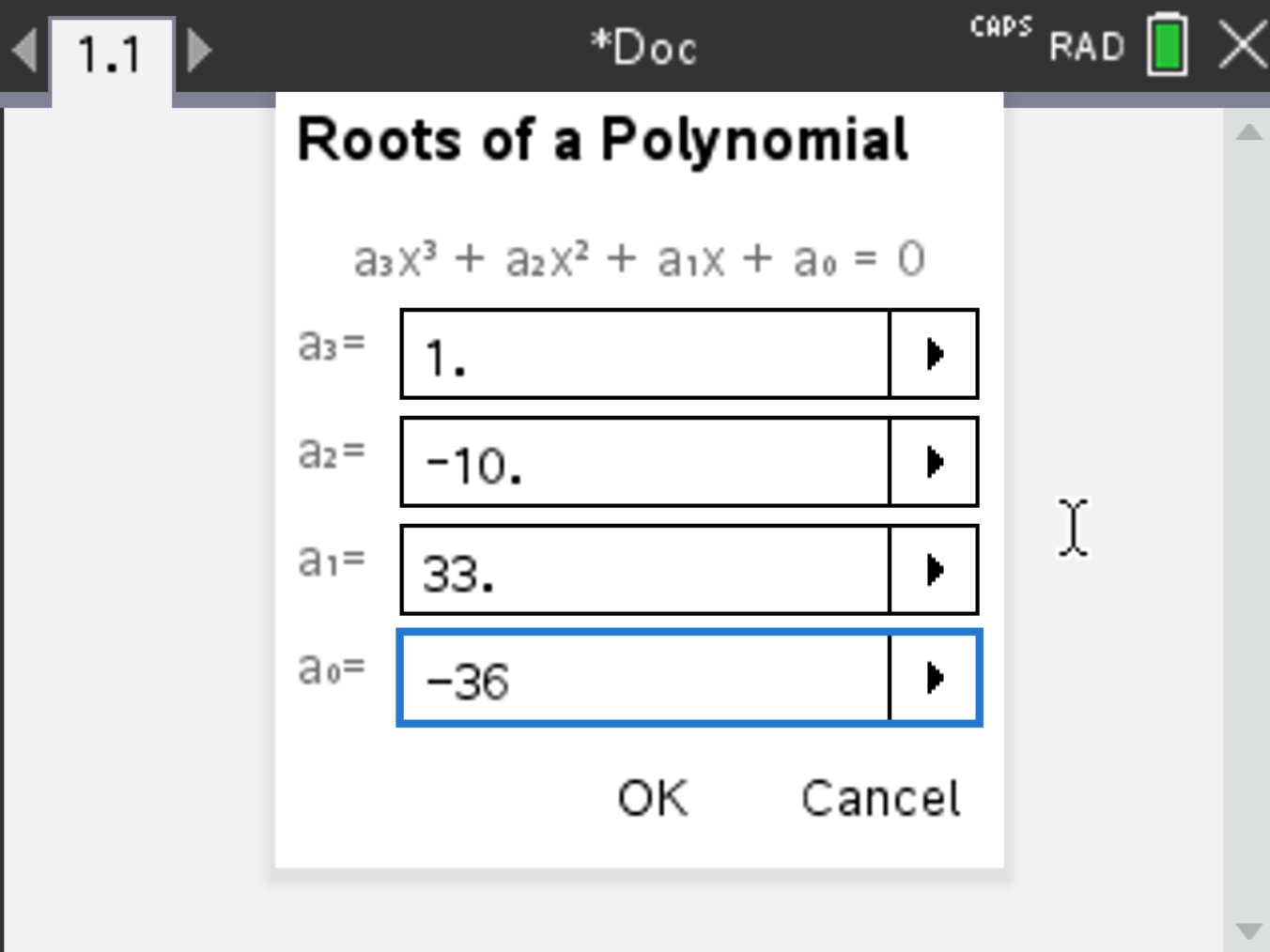
The order is the biggest power of \(x\) in the equation.
 . The results should be 3 and 4:
. The results should be 3 and 4:
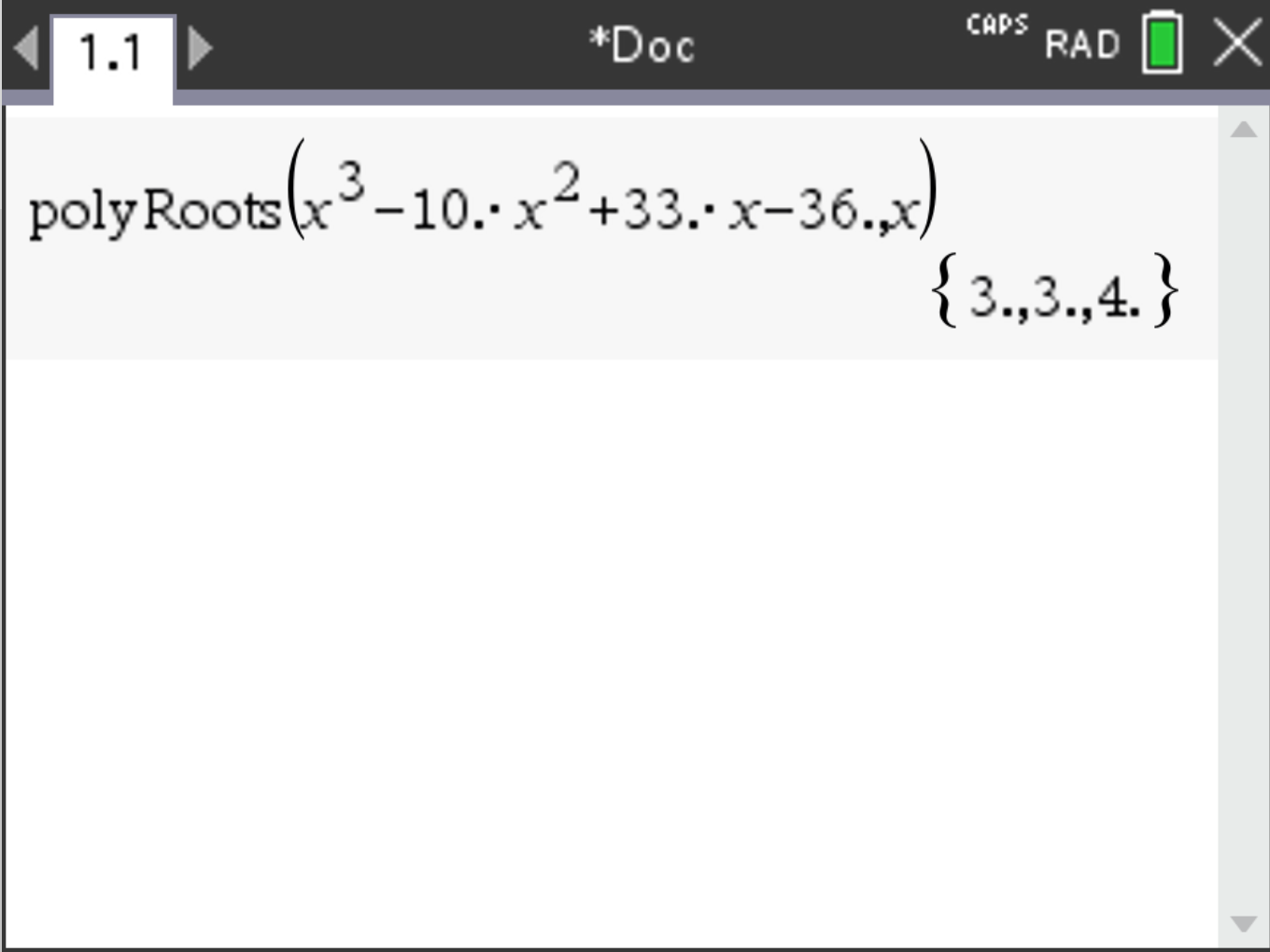
\(3\) appears twice because \(x^3 - 10x^2 + 33x - 36 = (x - 3)(x - 3)(x - 4)\).