Consider the complex numbers \( 3 + 4i \) and \( 2 + 5i \).

1. Suppose you want to add them. For this, just add them as you would add real numbers:

   The result should be \( 5 + 9i \).

2. Suppose you want to multiply them. Put each number in brackets and multiply each bracket:

   

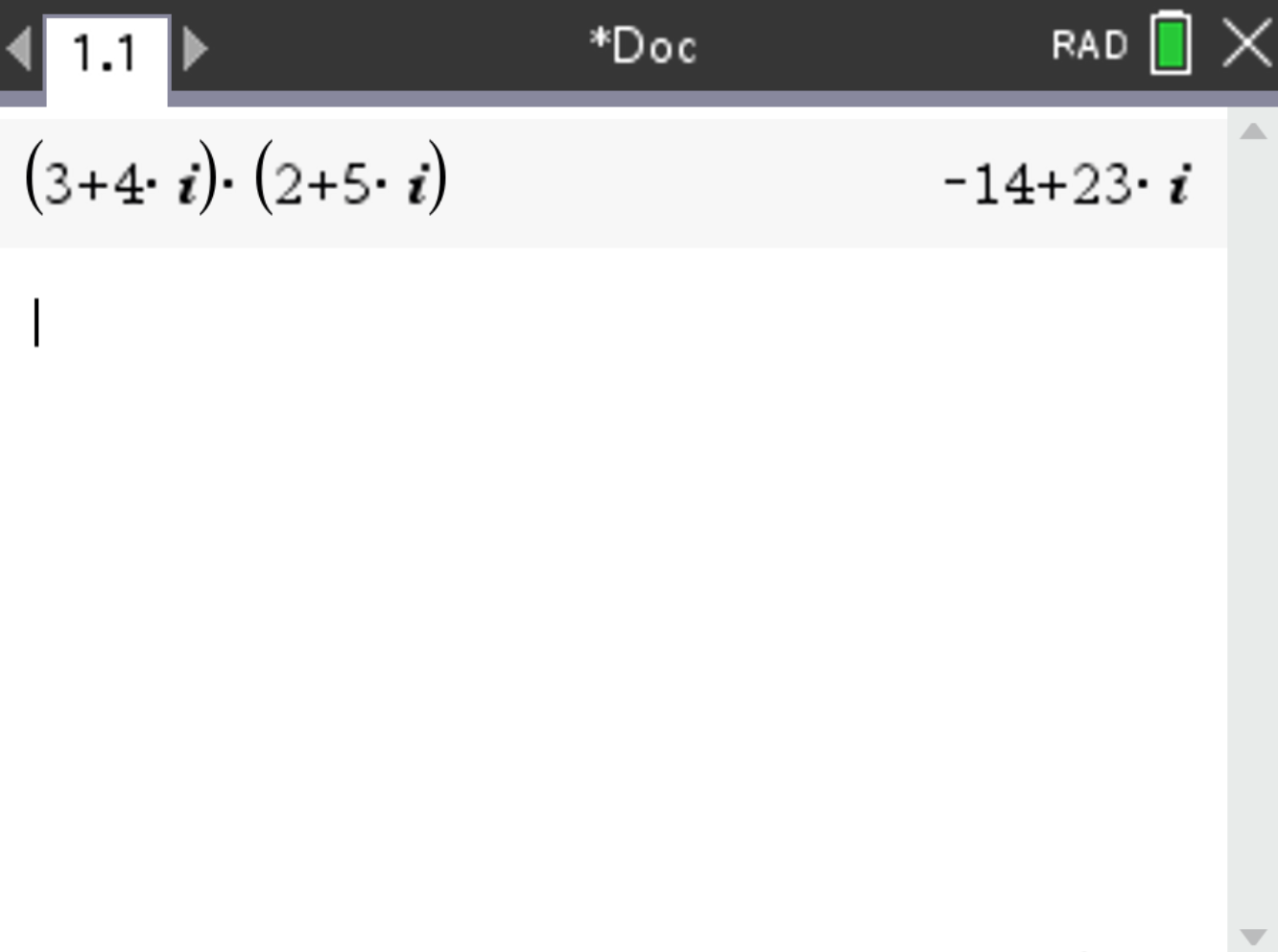
   The result should be \( -14 + 23i \).

3. Suppose you want to divide them. Display a fraction by pressing and select . Put the numbers in each part of the fraction:

   

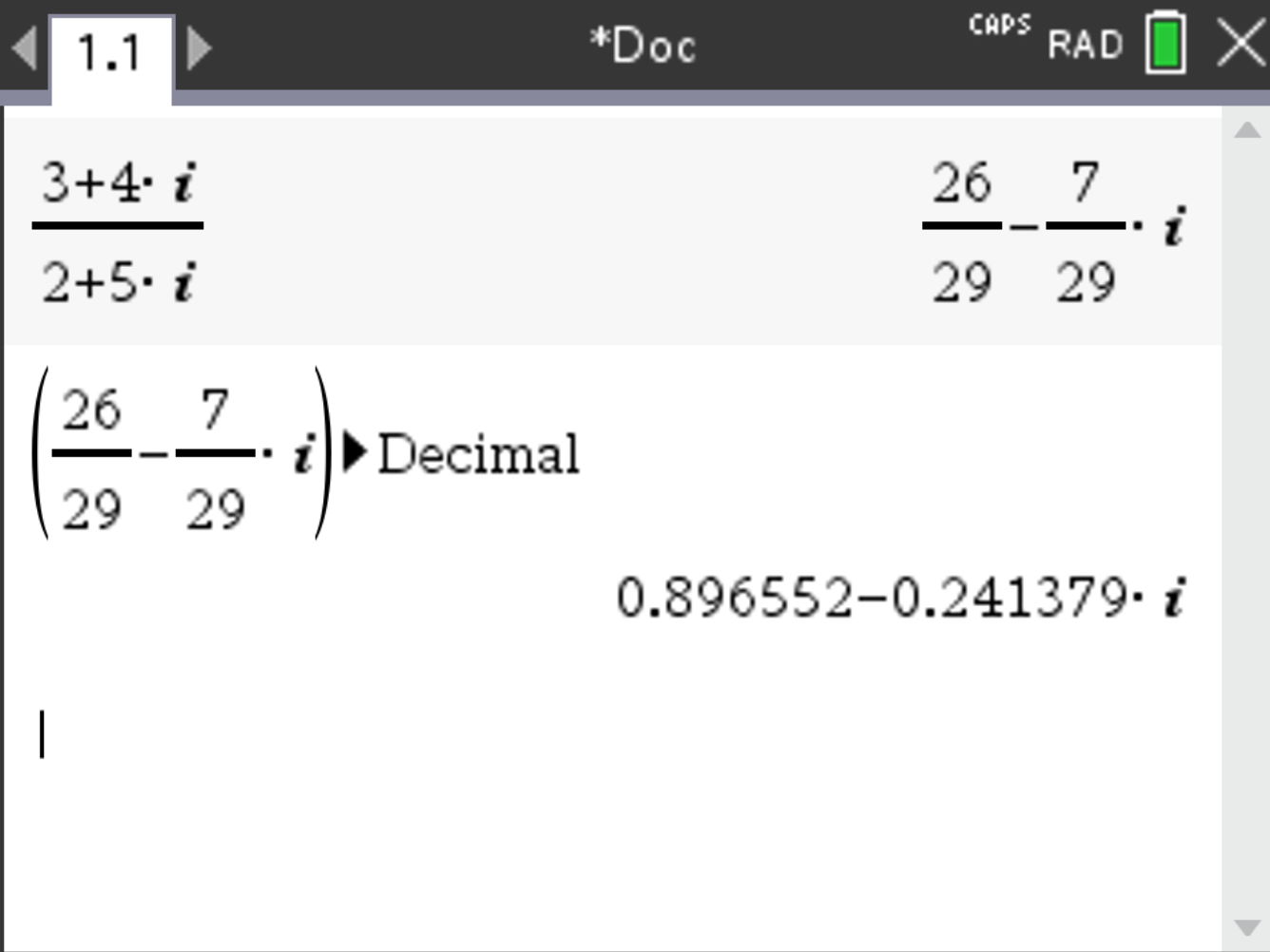
   The result should be approximately \( 0.897 - 0.241i \) or \( \frac{26}{29} - \frac{7}{29}i \).

   If you want to switch from fraction to decimal writing, press and select Number > Convert to Decimal.

Suppose you have to solve the equation \( x^2 + x + 1 = 0 \)

1. Ensure the right-hand side is \( 0 \).
2. Press , select Algebra > Complex > Solve, and the command csolve() will appear.
3. Enter the equation and the variable of interest after a comma inside the brackets.
4. Press . The solutions are displayed :

   

   The results should be \( x_1 = -\frac{1}{2} + \frac{\sqrt{3}}{2}i \) and \( x_2 = -\frac{1}{2} - \frac{\sqrt{3}}{2}i \) or in decimal form (rounded): \( x_1 = -0.5 + 0.866i \) and \( x_2 = -0.5 - 0.866i \).

   To change from fraction to decimal, press and select Number > Convert to Decimal.