Create a new document and select Add Lists & Spreadsheet. Fill the list A with the x-values, and the list B with the y-values.

1. Press and select Statistics > Stat Calculations > Two-Variable Statistics. Fill the parameters as follows:

   

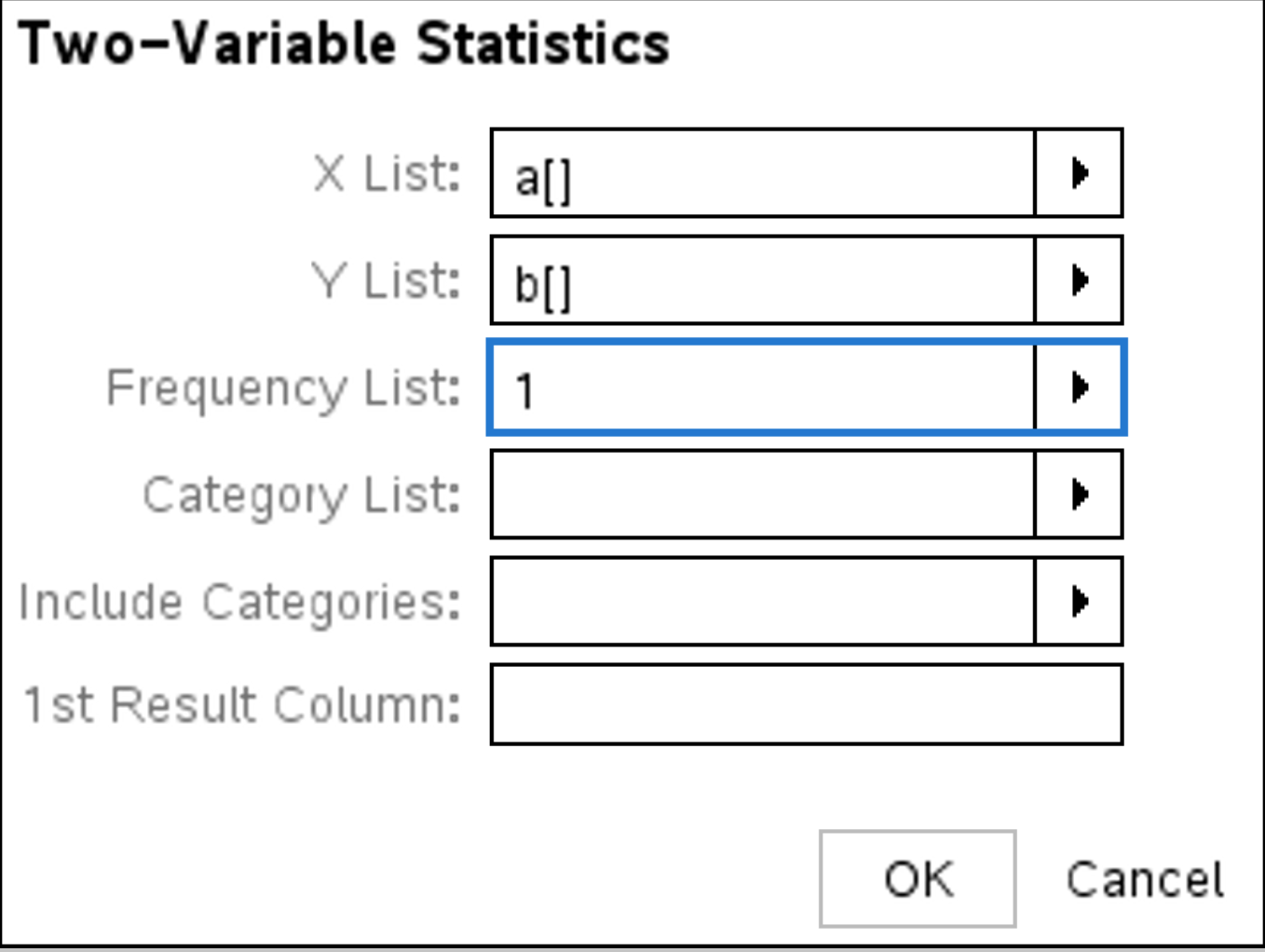
2. Press . The results are displayed in the table and should be \( \bar{x} = 7.23 \) and \( \bar{y} = -5.93 \).

1. Press and select Statistics > Stat Calculations > Linear Regression (\( ax + b \)).

   Choose the parameters as follows:

   

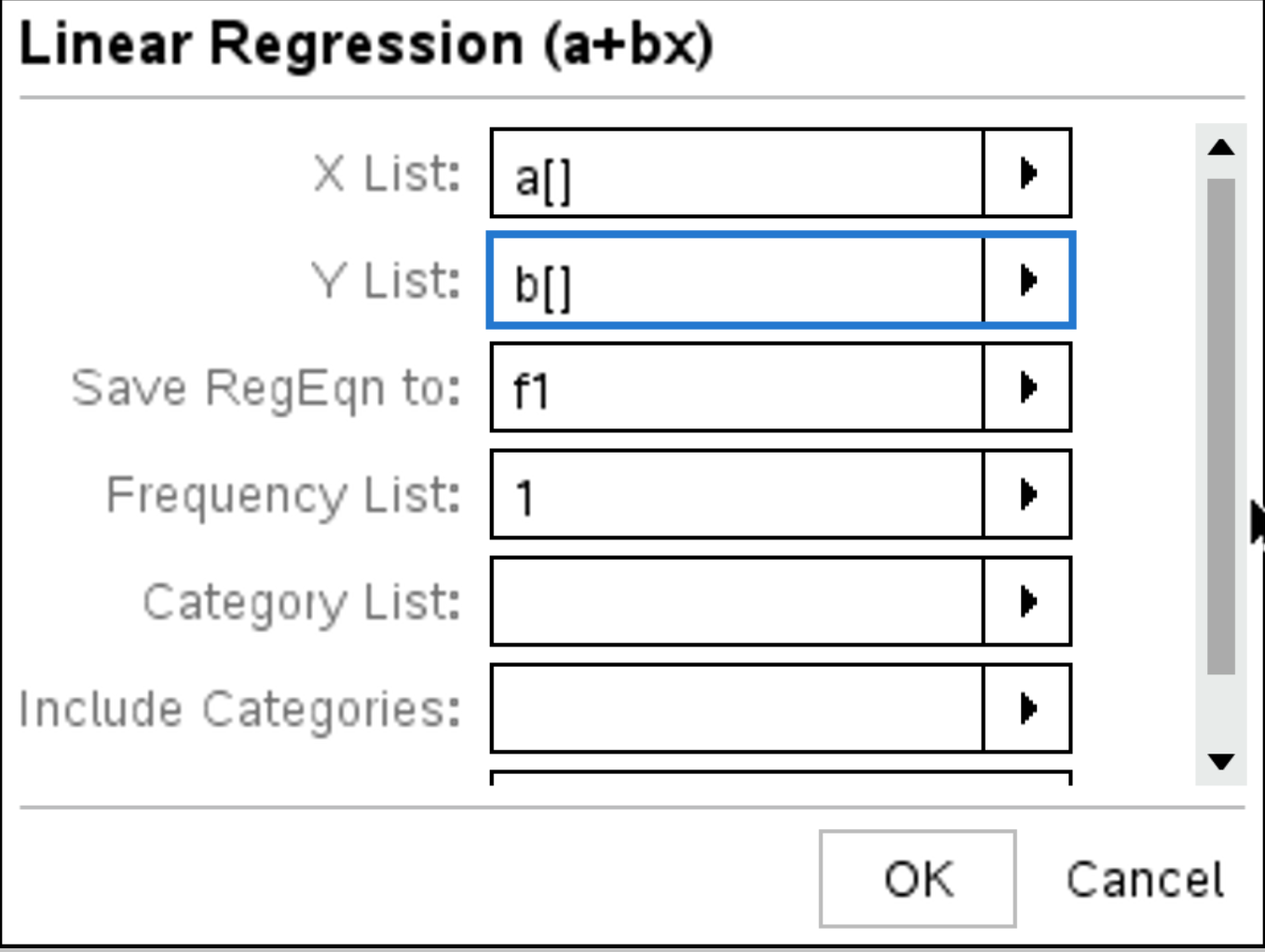
2. Press . The following result should appear:

   

1. Press and select Add Data & Statistics.
2. In the y-axis name, select stat.yreg. In the x-axis name, select stat.xreg.

   

3. Choose an appropriate window to have all the points fit nicely on the screen. Here, we chose \( X_{\text{min}} = -5 \), \( X_{\text{max}} = 18 \), \( Y_{\text{min}} = -30 \), and \( Y_{\text{max}} = 15 \).
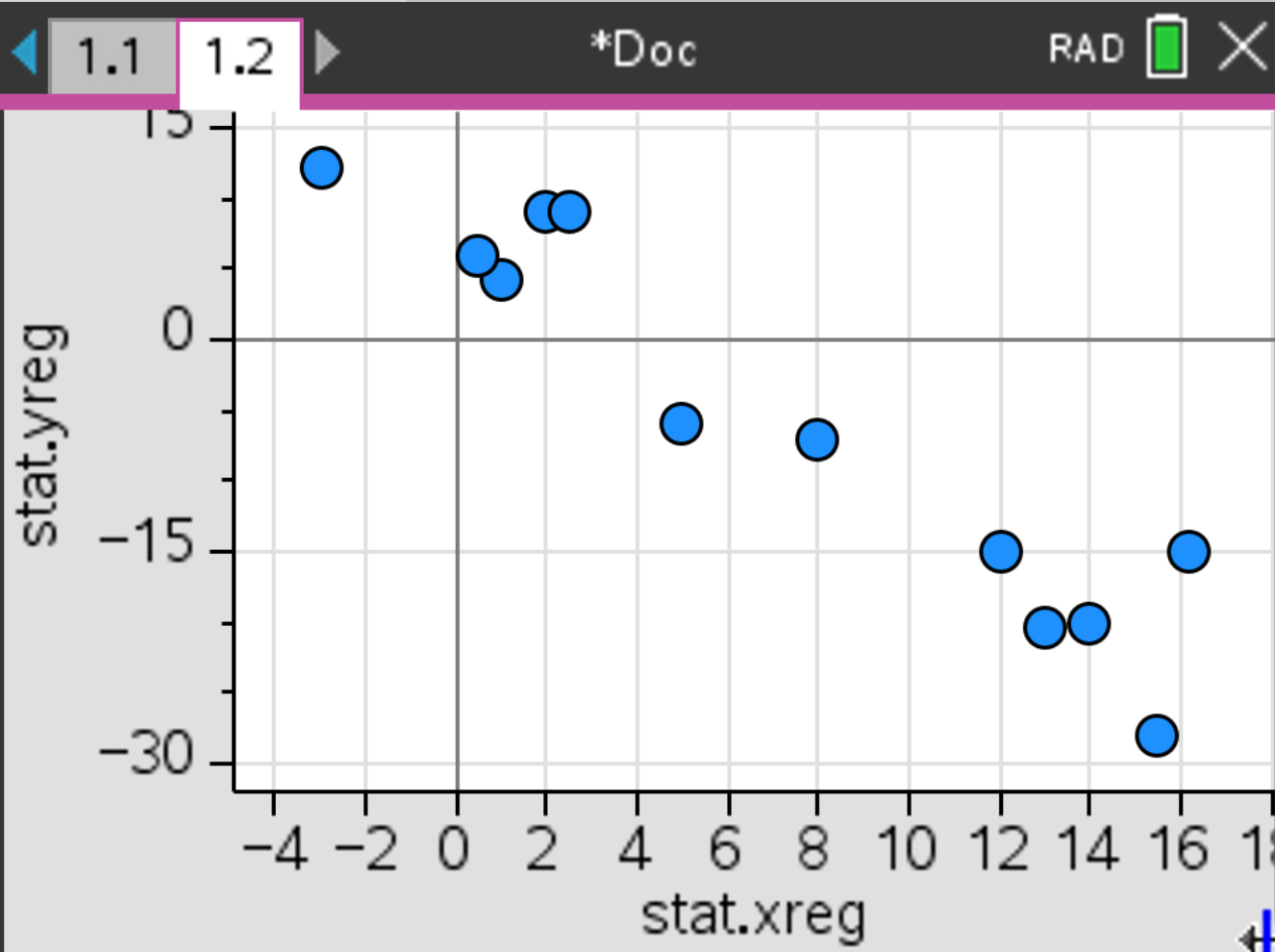
4. Press and select Analyze > Regression > Show Linear (\( ax+b \)). Press .