Suppose you want to evaluate \( \frac{df}{dx} \) at \( x = 3 \) for the following function:

\[ f(x) = \frac{x^2 - 2x + 2}{x^3} \]

1. Create a new document and select Add Calculator.
2. Enter f(x), press , then . Write the expression of the function.
3. Press and select Calculus > Derivative at a Point.
4. Enter x as the Variable and 3 as the Value. Press . Write f(x) inside the brackets. Press

   

   The result should be \( -0.037 \) (rounded). Thus, \( f'(3) = -0.037 \).

Suppose you want to draw the graph of \( \frac{df}{dx} \) for the following function:

\[ f(x) = \frac{x^2 - 2x + 2}{x^3} \]

1. Create a new document and select Add Calculator.
2. Enter f(x), press , then . Write the expression of the function. Press .
3. In the following line, write fd(x). Press and to define the function. Then, press , select Calculus > Derivative, and write f(x) inside the brackets. Press . The derivative is displayed.

   

4. Open a new page by pressing and . Select Add Graphs.
5. Write f1(x) = fd(x) and press .
6. Choose an appropriate window. For example:
   • \( X_{\text{min}} = -10 \)
   • \( X_{\text{max}} = 10 \)
   • \( Y_{\text{min}} = -10 \)
   • \( Y_{\text{max}} = 10 \)

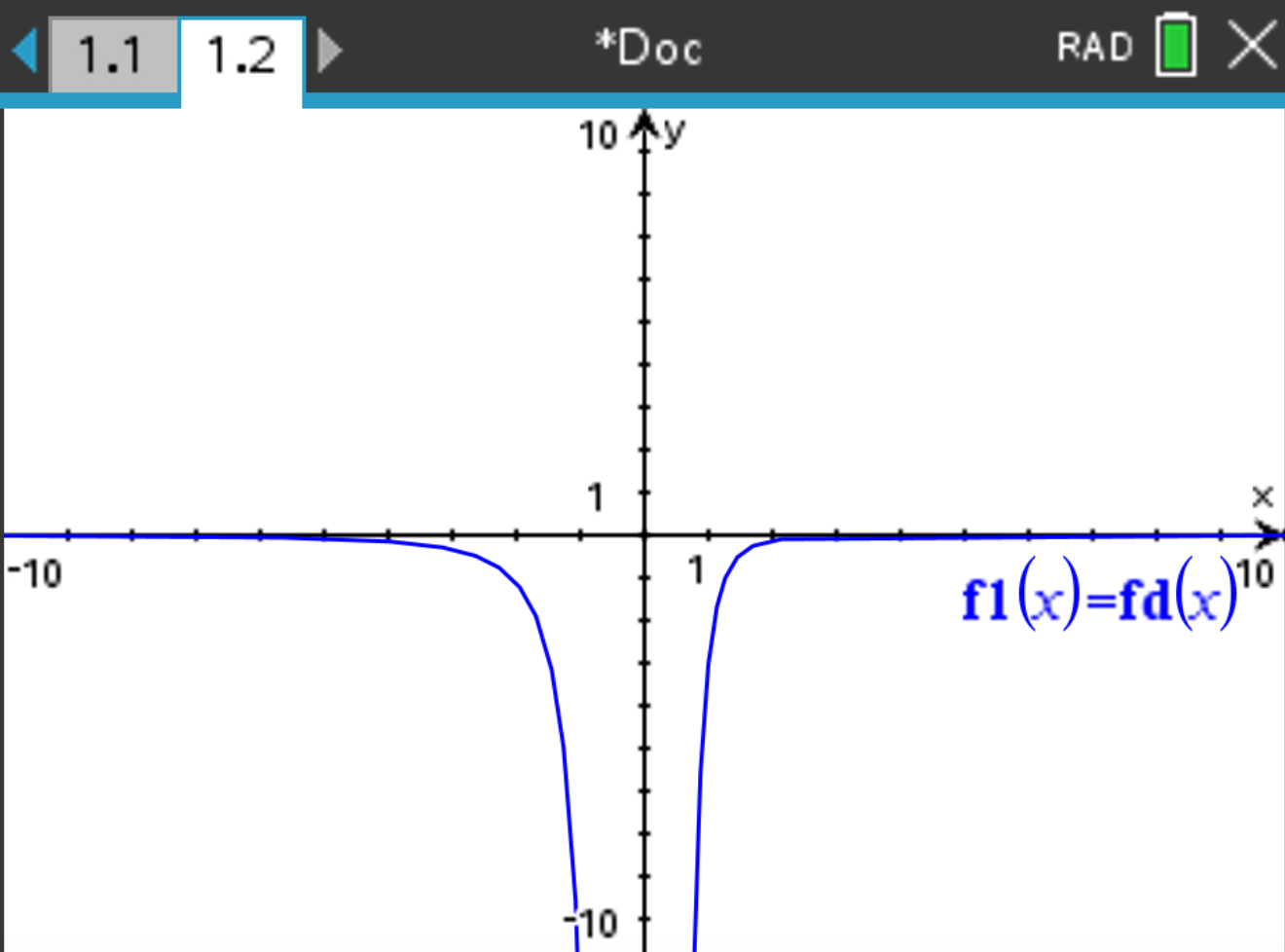
   The graph should display as follows: