TI-NSpire Manual

Compute \( P(X \leq a) \) with normal CDF function

In the following subsections, we will only compute probabilities involving “≤”. However, since the normal distribution is continuous, you could replace all the “≤” by a “<”, and the result would be the same.

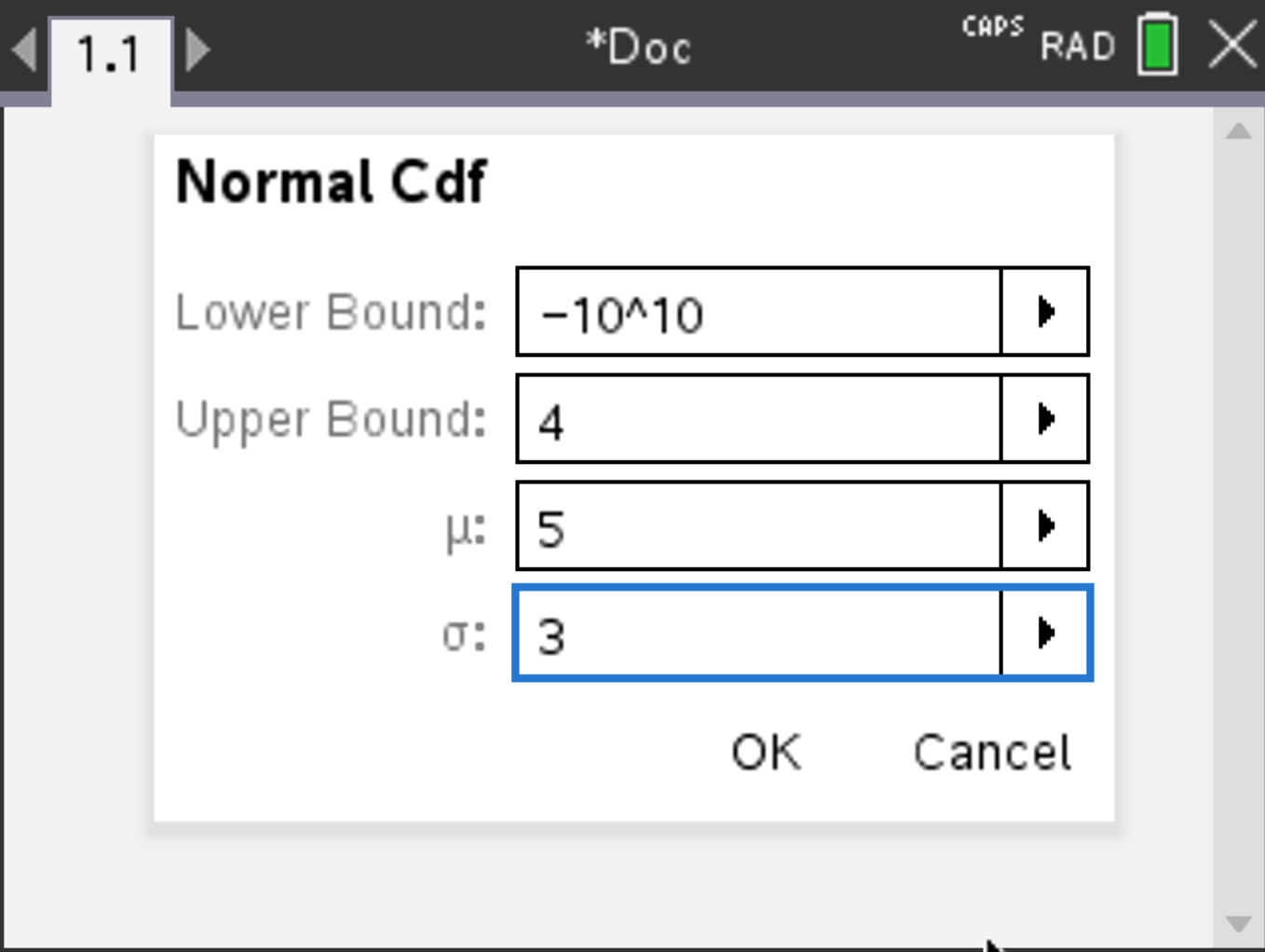
Consider a random variable \( X \sim N(5, 3^2) \). Suppose you want to compute \( P(X \leq 4) \).

Press , select Probability > Distributions > Normal CDF, choose a huge negative value for lower (like \( -10^{10} \)), and upper: 4 (here \( \mu = 5 \) and \( \sigma = 3 \)).
Press .
The result should be \( 0.369 \) (rounded).

Compute \( P(X \geq a) \) with normal CDF function

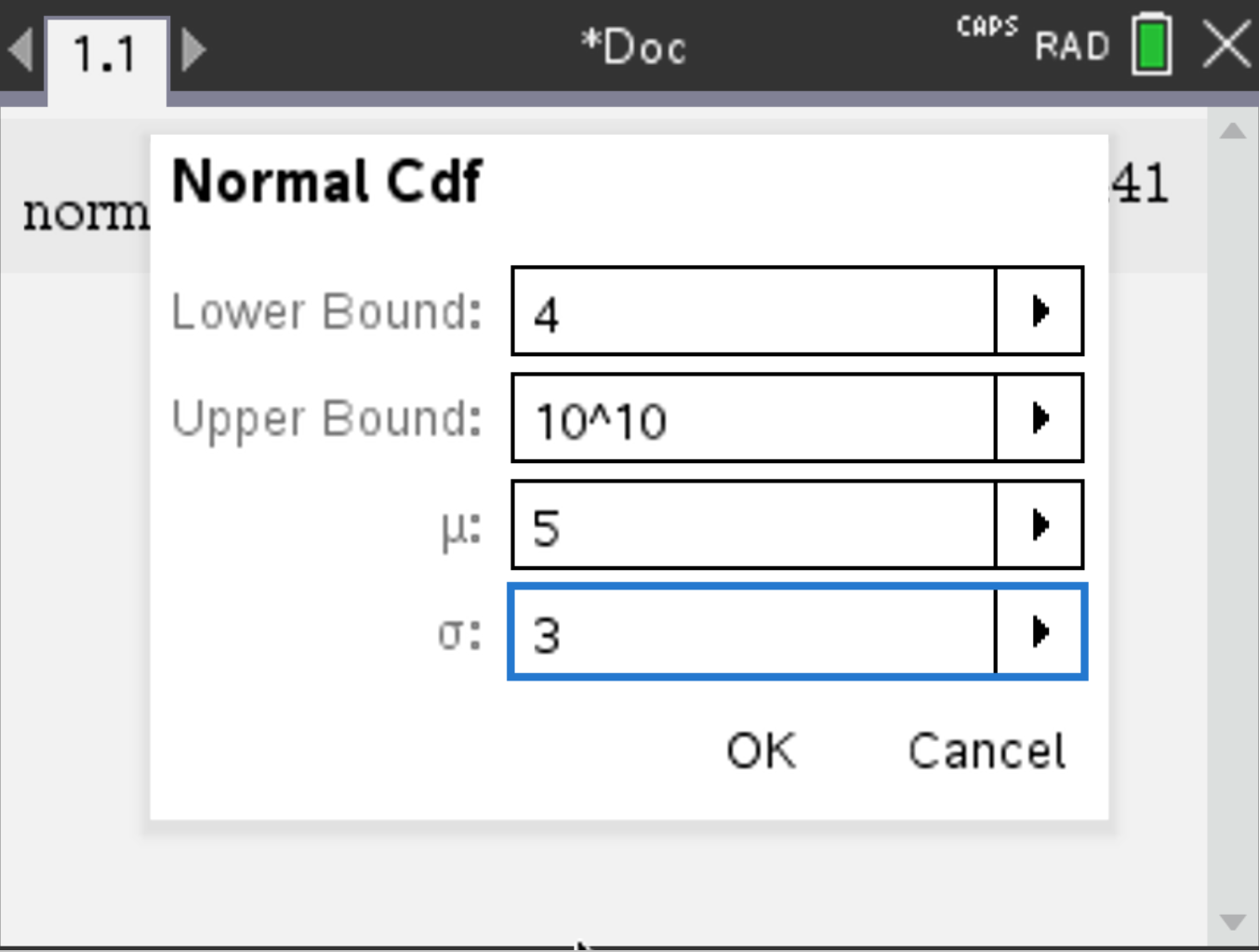
Consider a random variable \( X \sim N(5, 3^2) \). Suppose you want to compute \( P(X \geq 4) \).

Press , select Probability > Distributions > Normal CDF, choose a huge positive value for upper (like \( 10^{10} \)), and lower: 4 (here \( \mu = 5 \) and \( \sigma = 3 \)).
Press .
The result should be \( 0.631 \) (rounded).

Compute \( P(a \leq X \leq b) \) with normal CDF function

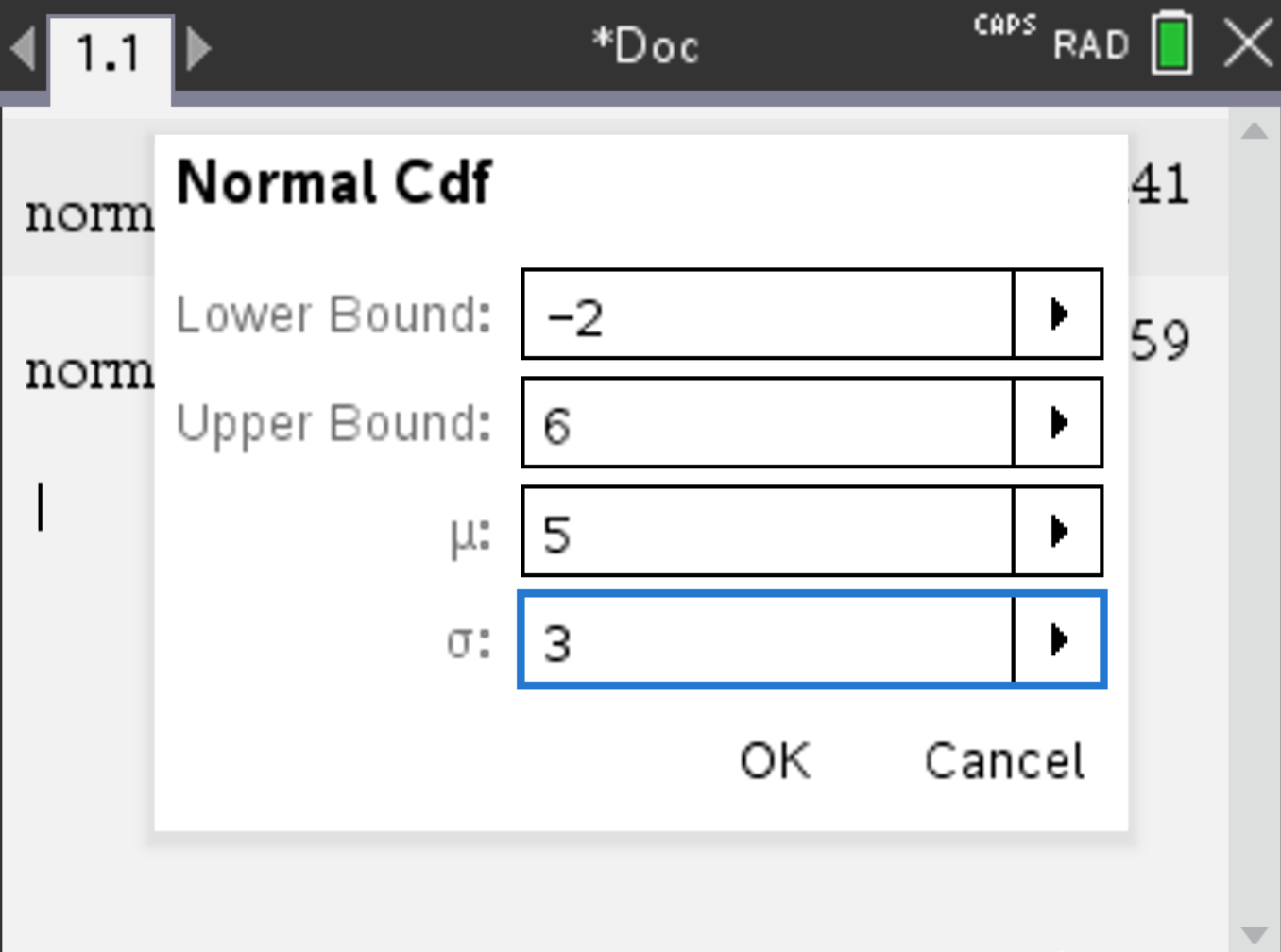
Consider a random variable \( X \sim N(5, 3^2) \). Suppose you want to compute \( P(-2 \leq X \leq 6) \).

Press , select Probability > Distributions > Normal CDF, choose upper: 6, and lower: -2 (here \( \mu = 5 \) and \( \sigma = 3 \)).
Press .
The result should be \( 0.621 \) (rounded).

Find \( x \) when \( P(X \leq x) = c \) with inverse normal function

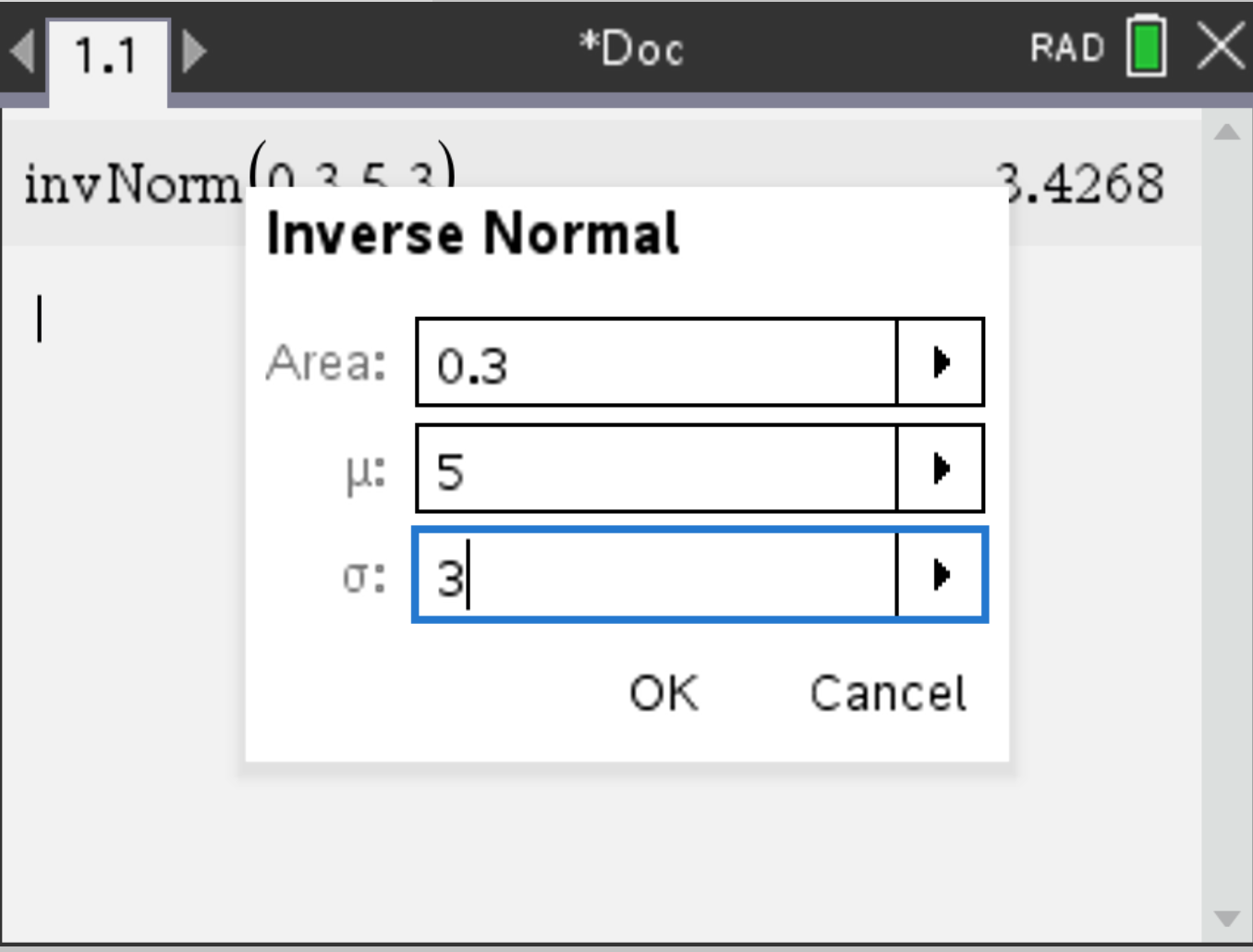
Consider a random variable \( X \sim N(5, 3^2) \). Suppose you want to know for what \( x \) we have \( P(X \leq x) = 0.3 \).

Press , select Probability > Distributions > Inverse Normal, choose Area: 0.3 (here \( \mu = 5 \) and \( \sigma = 3 \)).
Press .
The result should be \( x = 3.43 \) (rounded).

Plot a normal distribution

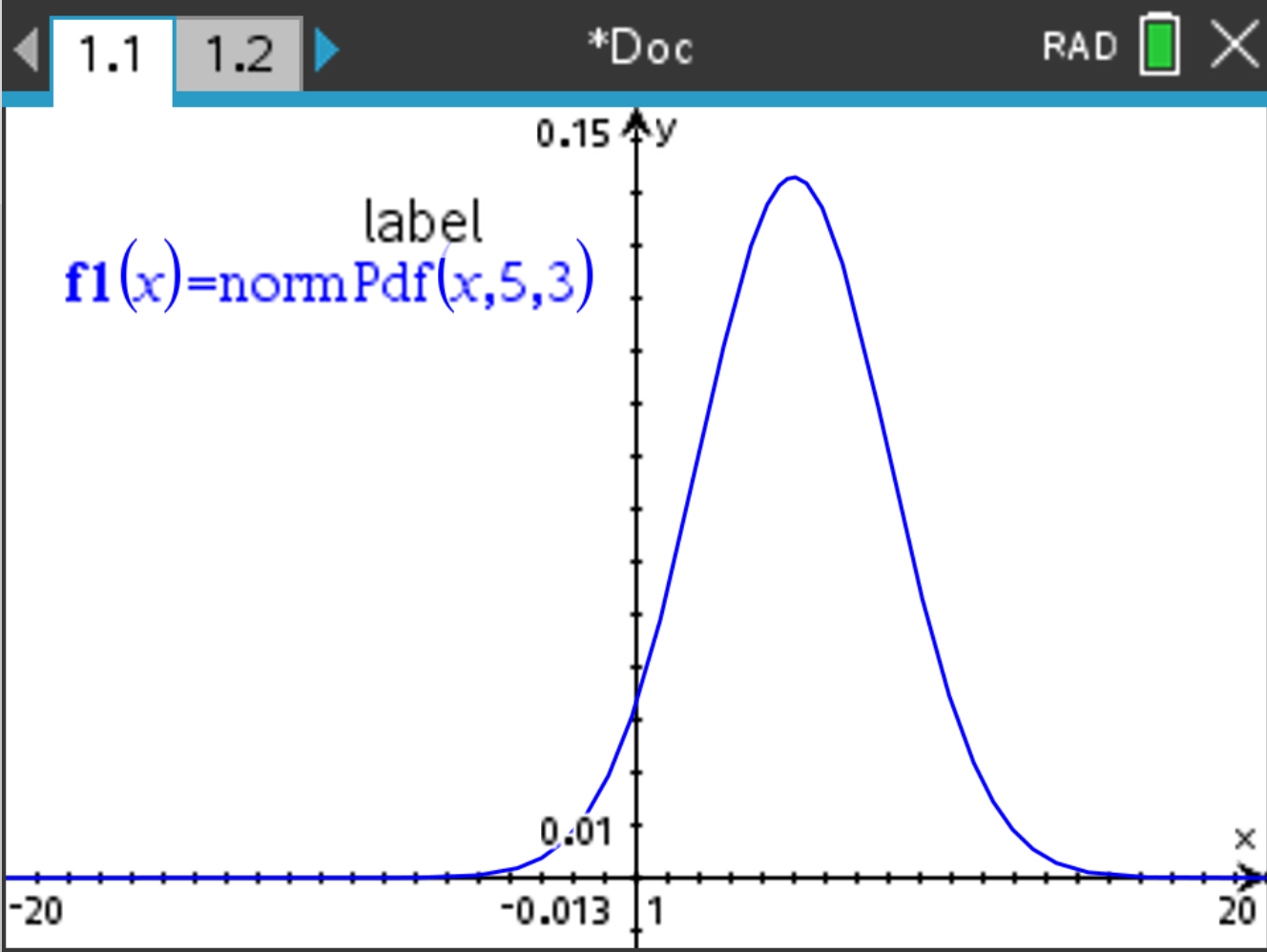
Consider a random variable \( X \sim N(5, 3^2) \).

Create a new document and select Add Graphs.
Enter f1(x)=normPdf(x,5,3). Press .
Choose an appropriate window. Here, we chose the following:
The graph should look like this: