Suppose you want to compute the following definite integral:

\[ \int_0^1 (x^3 + 3x + 1) \, dx \]

In the main screen, press and select . Fill the parameters as follows:

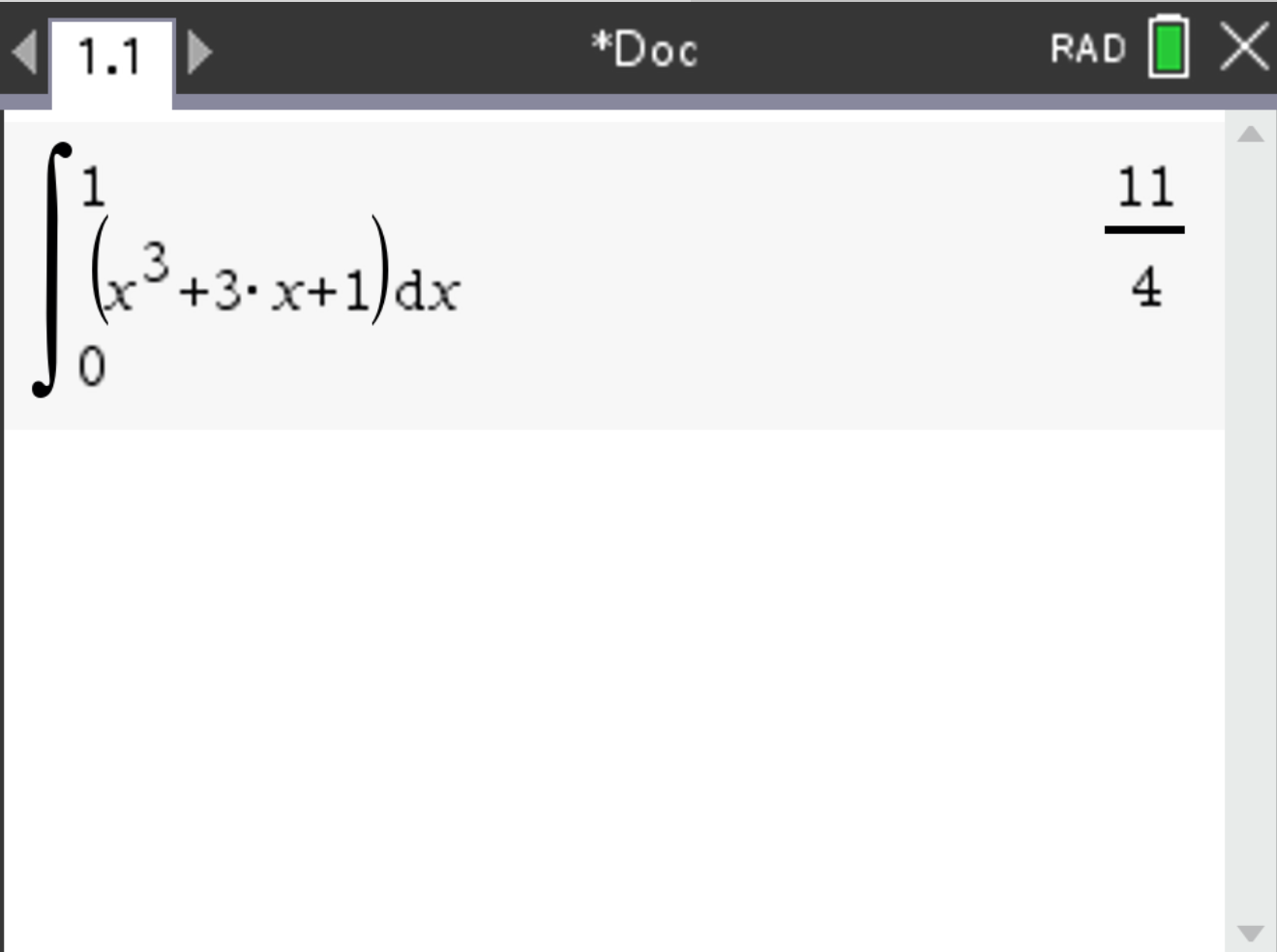
The result should be \( 2.75 \).

Suppose you want to draw the area between \( x = 0 \) and \( x = 1 \) of the following function:

\[ f(x) = x^3 + 3x + 1 \]

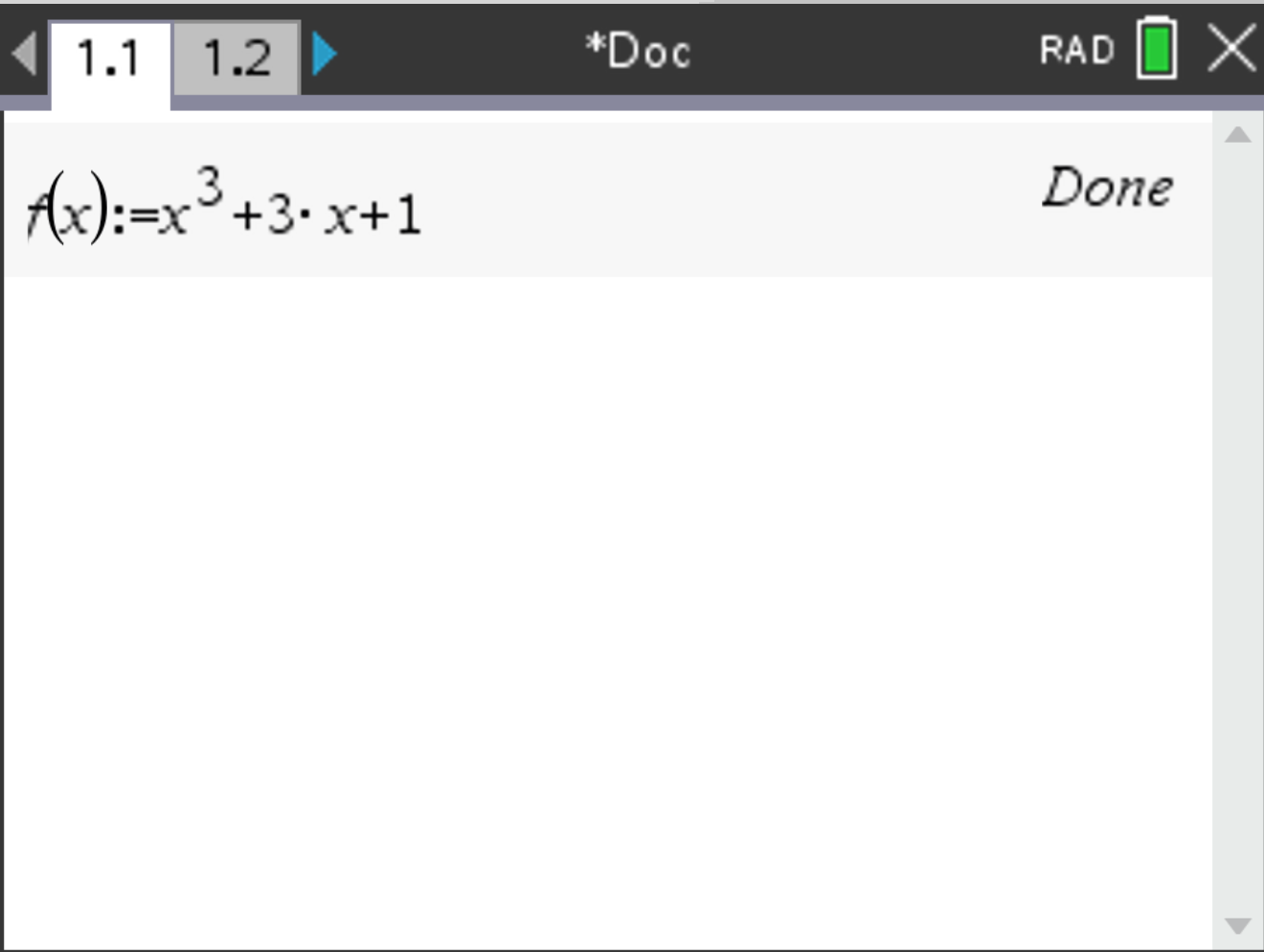
1. Enter the function by typing f(x). Then press and . Write the expression for the function.

   

2. Open a new page by pressing and . Select Add Graphs. Enter f1(x)=f(x), then press .
3. Choose an appropriate window. Here, we chose:
   • \( X_{\text{min}} = -1 \)
   • \( X_{\text{max}} = 3 \)
   • \( Y_{\text{min}} = -1 \)
   • \( Y_{\text{max}} = 30 \)
4. Press and select Analyze Graph > Integral. Type the lower bound as \( 0 \) and the upper bound as \( 1 \), then press . Same for upper bound which is 1. The following should be displayed:

   

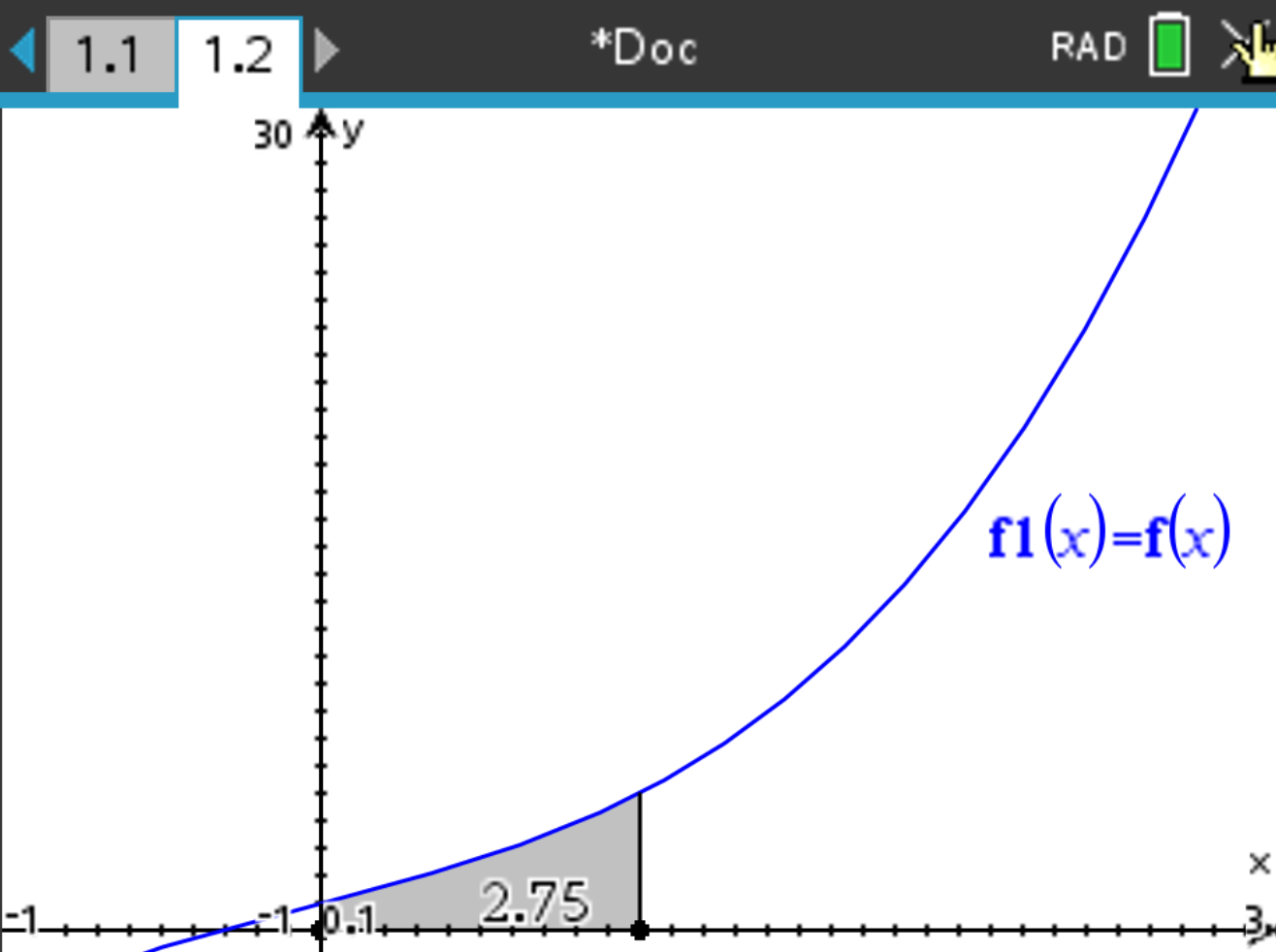
   The graph should display the area under the curve, which is \( 2.75 \), highlighted in grey.