Consider the differential equation:
\[ \frac{dy}{dx} = x - y^2 \]
With the initial condition \( y(1.3) = 2.35 \), we approximate \( y(2.2) \) rounded to four significant figures, using step size \( h = 0.1 \).
We want to iterate over the x′s and the y′s. The Euler method tells us to choose the sequences defined by:
\[ x_{n+1} = x_n + 0.1, \quad y_{n+1} = y_n + 0.1 \cdot (x_n - y_n^2) \]
The initial conditions are \( x_1 = 1.3 \) and \( y_1 = 2.35 \).

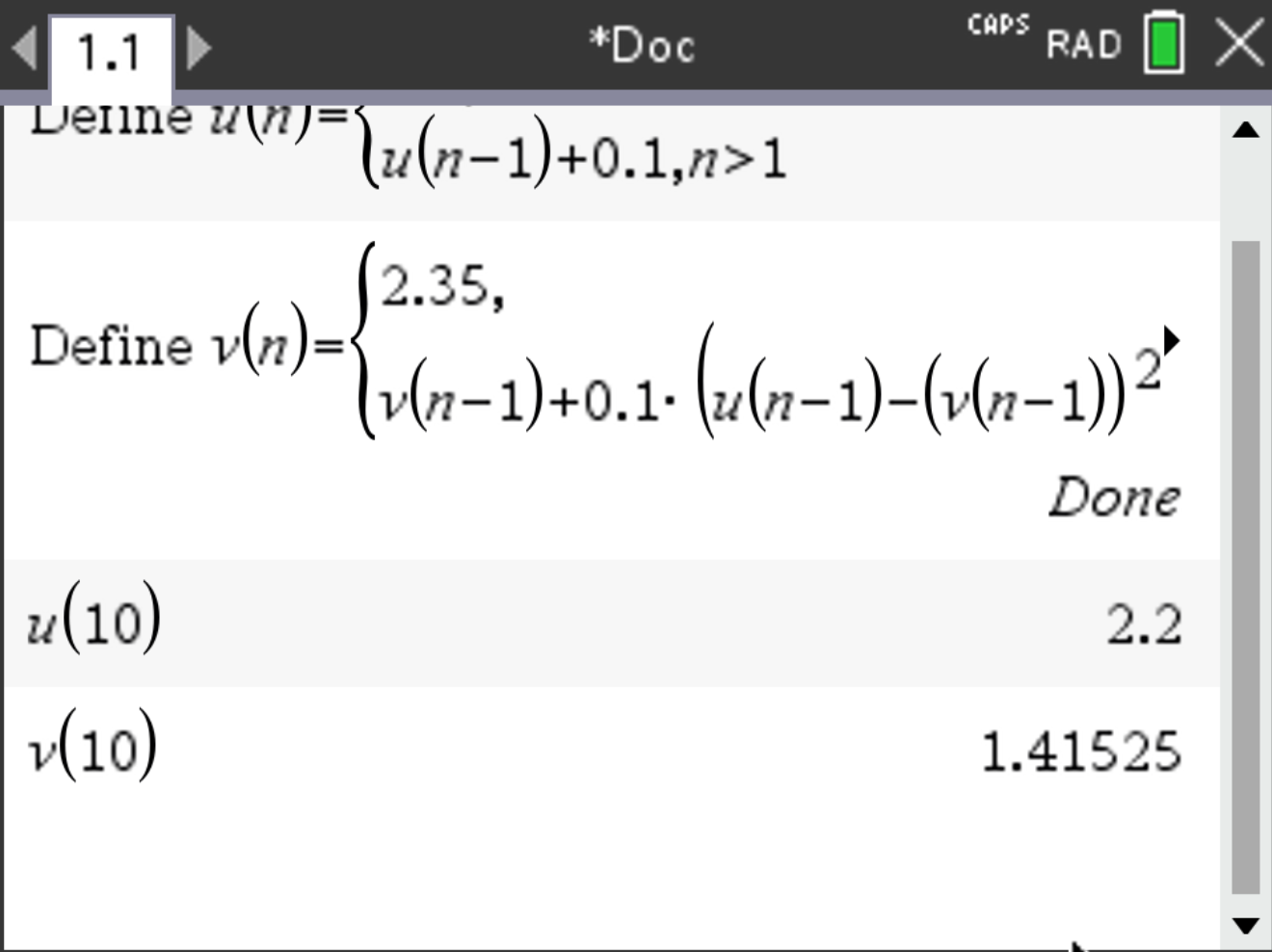
In the TI-Nspire, sequences are represented as \( u(n) \) for \( x_n \) and \( v(n) \) for \( y_n \). For example, \( u(2) = x_2 = 1.4 \) and \( v(2) = y_2 \).
 , and select Add Calculator.
, and select Add Calculator.
 and select Actions > Define.
and select Actions > Define.

To compute \( y(2.2) \), recall that \( u(10) = x_{10} = 2.2 \). Therefore, \( v(10) = y_{10} \approx y(2.2) \).