Suppose you want to find graphically all the turning points of the following function:

\[ f(x) = x^3 - 6x^2 + 11x - 6 \]

1. Create a new document and select Add Graphs. Enter the function into f1(x).
2. Enter f2(x) = \frac{df1(x)}{dx} by pressing and to graph the derivative of the function. Select only f2(x) to show only the derivative.
3. Find the zeros of the derivative:
   1. Press and select Analyze Graph > Zero.
   2. Select lower and upper bounds between the crossing of the x-axis.
   3. Press . Repeat this process for the second zero.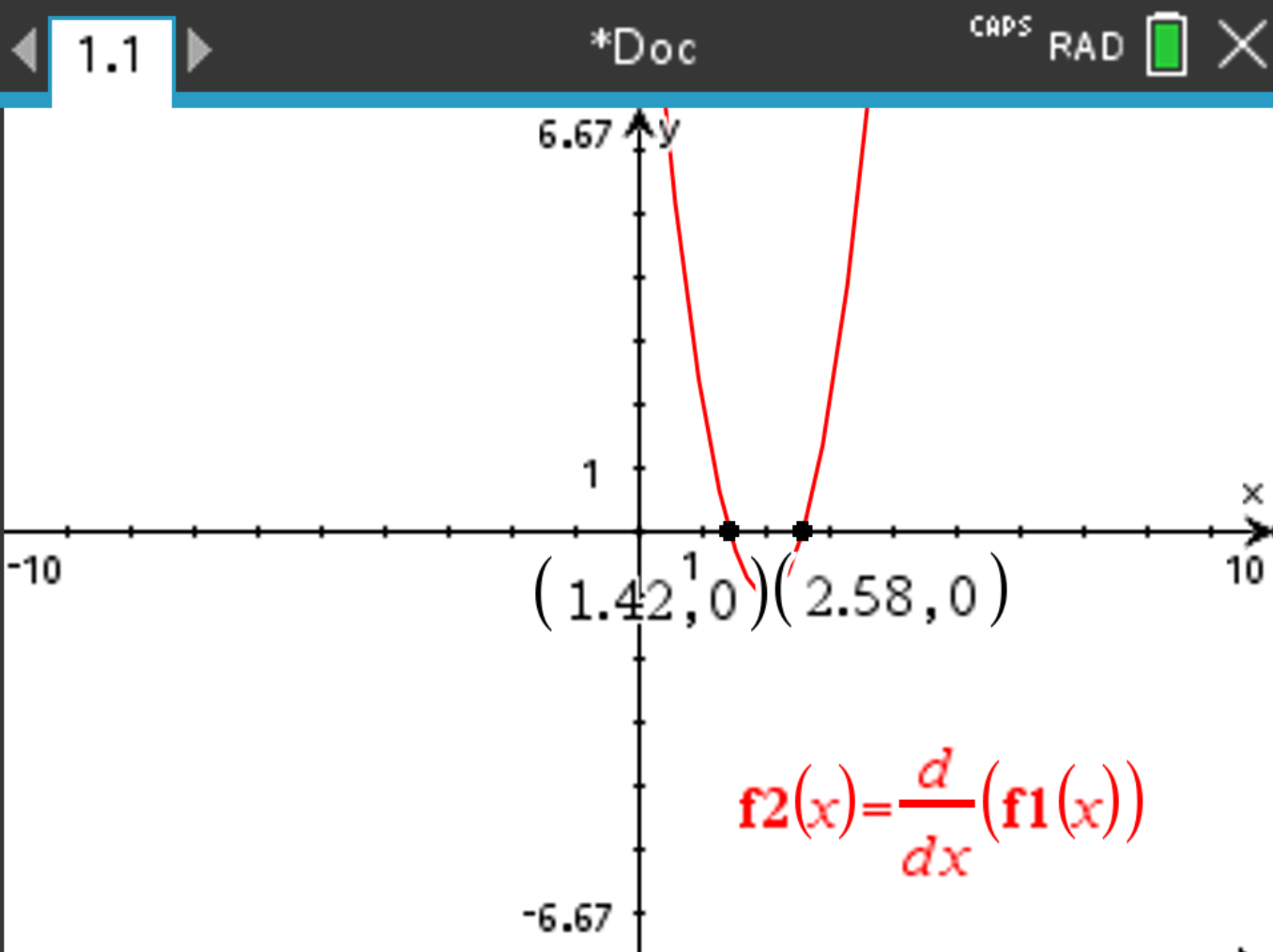

   

   The results should be \( x = 1.42 \) and \( x = 2.58 \) (rounded).