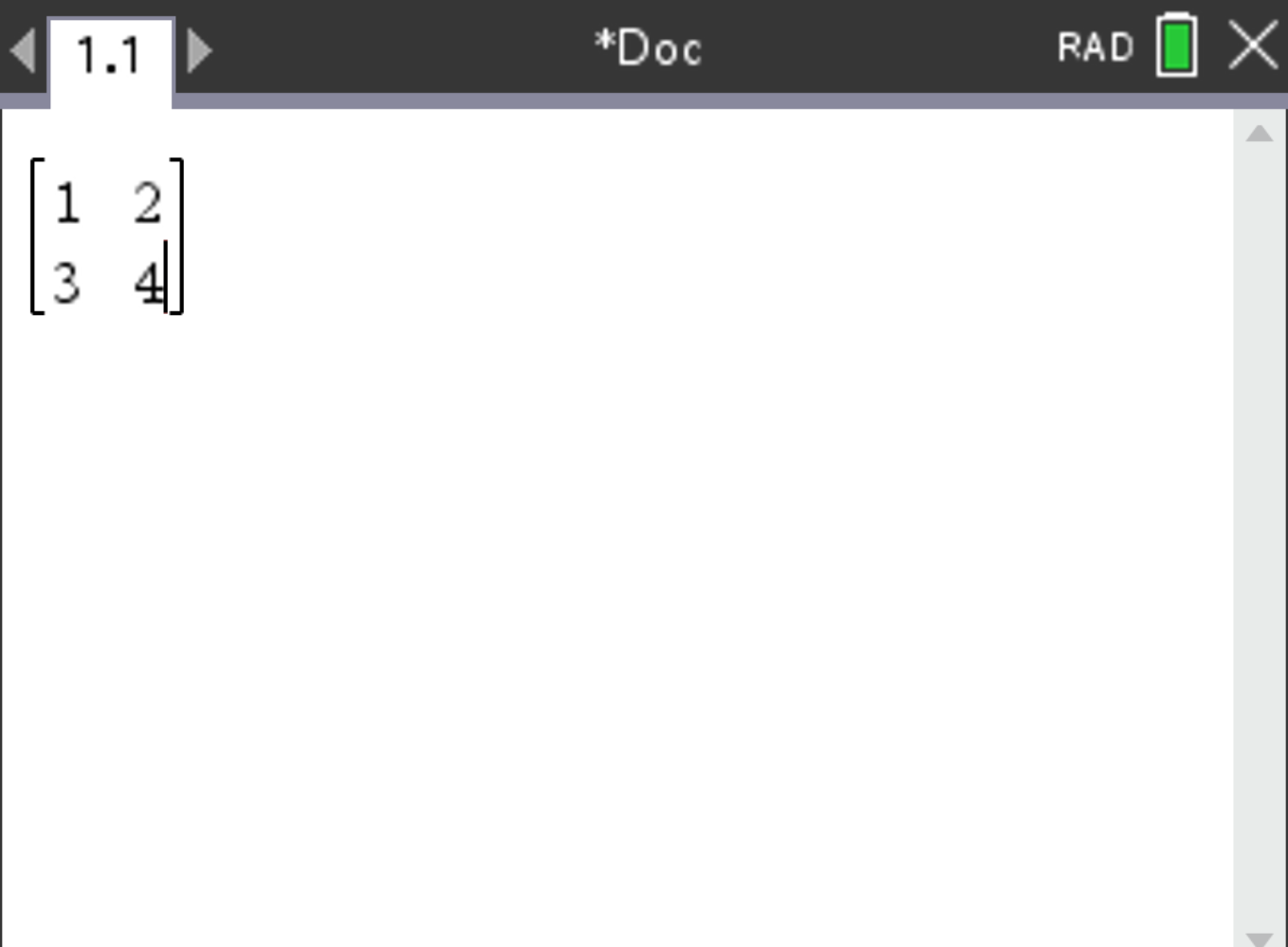
Consider the matrix:

\[ \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \]

There are two ways to enter a matrix in your calculator.

1. First Way: If you just want to use the matrix for one computation, press and select Matrix & Vector > Create > Matrix. Choose the proper dimensions (here, Number of rows = 2 and Number of columns = 2), and press . You can then fill the matrix as follows:

   

2. Second Way: If you want to store the matrix in the calculator, do the same process. Then, press and . Enter the name of the matrix, here it is A.

   

Consider the matrix:

\[ A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \]

Once you have entered it ( see above), you can display it in the main screen by entering A and pressing .

The matrix is displayed.

Suppose you have two matrices:

\[ A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} , \quad B = \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix} \]

We can perform the following operations:

1. Addition: Enter A + B and press .

   

   The result is: \[ A + B = \begin{pmatrix} 6 & 8 \\ 10 & 12 \end{pmatrix} \]

2. Subtraction: Enter A - B and press . The result is: \[ A - B = \begin{pmatrix} -4 & -4 \\ -4 & -4 \end{pmatrix} \]
3. Multiplication: Enter A x B and press . The result is: \[ A * B = \begin{pmatrix} 19 & 22 \\ 43 & 50 \end{pmatrix} \]

Note: To perform matrix operations, ensure that the matrices are of compatible dimensions.

Identity and zero matrices are fundamental in matrix operations. Here’s how to create them:

1. Create an Identity Matrix:
   1. Press and select Matrix & Vector > Create > Identity.
   2. Enter the size of the matrix (e.g., 3 for a 3x3 identity matrix) and press .

   The result should be:

   \[ I = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \]

2. Create a Zero Matrix:
   1. Press and select Matrix & Vector > Create > Zero Matrix.
   2. Enter the dimensions of the matrix (e.g., 3 rows and 2 columns for a 3x2 zero matrix) and press .

   The result should be:

   \[ Z = \begin{pmatrix} 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{pmatrix} \]

Identity and zero matrices are useful for checking properties such as inverses and simplifying operations.

Consider the matrix:

\[ A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \]

To compute the determinant:

1. Enter the matrix ( see above)
2. Press and select Matrix & Vector > Determinant.
3. Enter A (or the matrix directly) and press .

   

   The result should be \( \text{det}(A) = 3 \).

Consider the matrix:

\[ A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \]

To compute the inverse:

1. Enter A^-1 (using the power key ).
2. Press . The following result should be displayed:

   

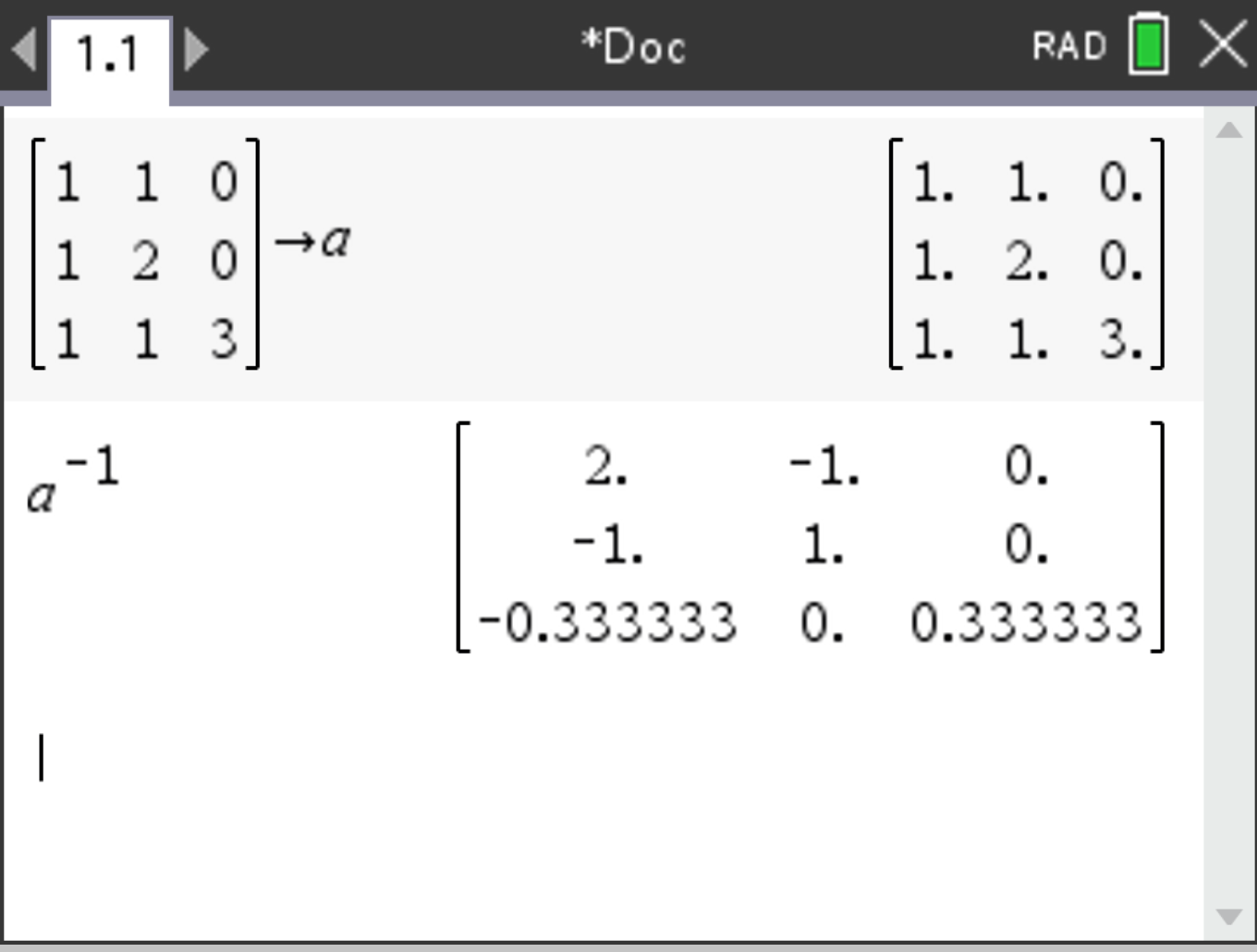
Note: The matrix must be square and have a non-zero determinant to have an inverse.