Suppose you want to graph \( (f \circ g)(x) \) for the following functions:

\[ f(x) = x^2 - 2x + 5, \quad g(x) = \frac{x + 3}{4} \]

1. Create a new document, press , and select Add Calculator.
2. Enter the two expressions \( f(x) \) and \( g(x) \), each on a different line:
   • Write f(x) and press .
   • Do the same for \( g(x) \).
3. Write f(g(x)) in a third line and press . The result is displayed.

   

4. To plot the function, open a new page by pressing and . Select Add Graphs.
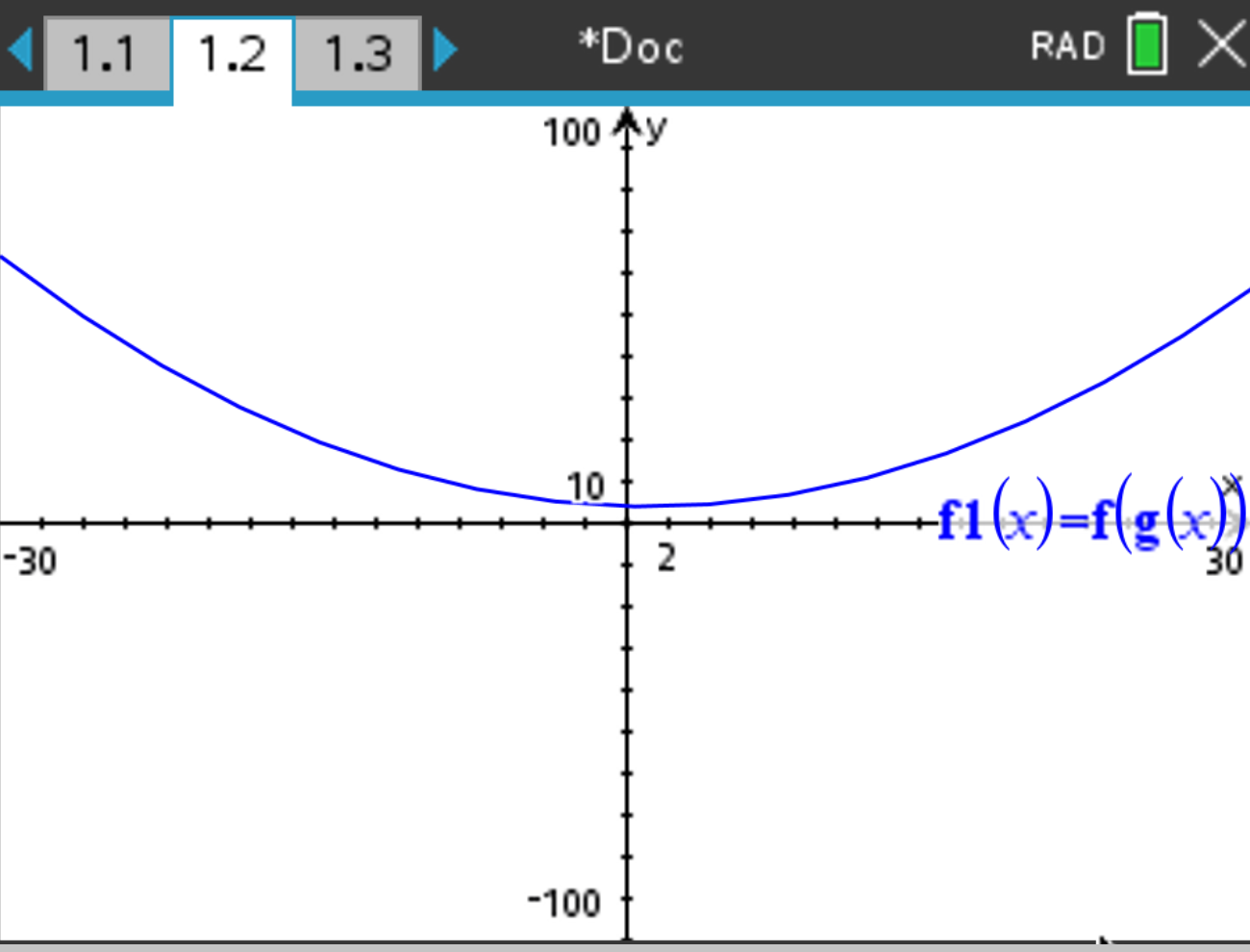
5. Write f1(x) = f(g(x)) and press .
6. Choose an appropriate window. Press and select Window/Zoom > Window Settings. Enter the appropriate values: \[ X_{\text{min}} = -30, \quad X_{\text{max}} = 30, \quad Y_{\text{min}} = -100, \quad Y_{\text{max}} = 100 \]

   

Suppose you want to evaluate \( (f \circ g)(1) \) for the following functions:

\[ f(x) = x^2 - 2x + 5, \quad g(x) = \frac{x + 3}{4} \]

1. Create a new document, press , and select Add Calculator.
2. Enter the two expressions \( f(x) \) and \( g(x) \), each on a different line:
   • Write f(x) and press and .
   • Do the same for \( g(x) \).
3. Write f(g(1)) in a third line and press . The result is displayed.

   

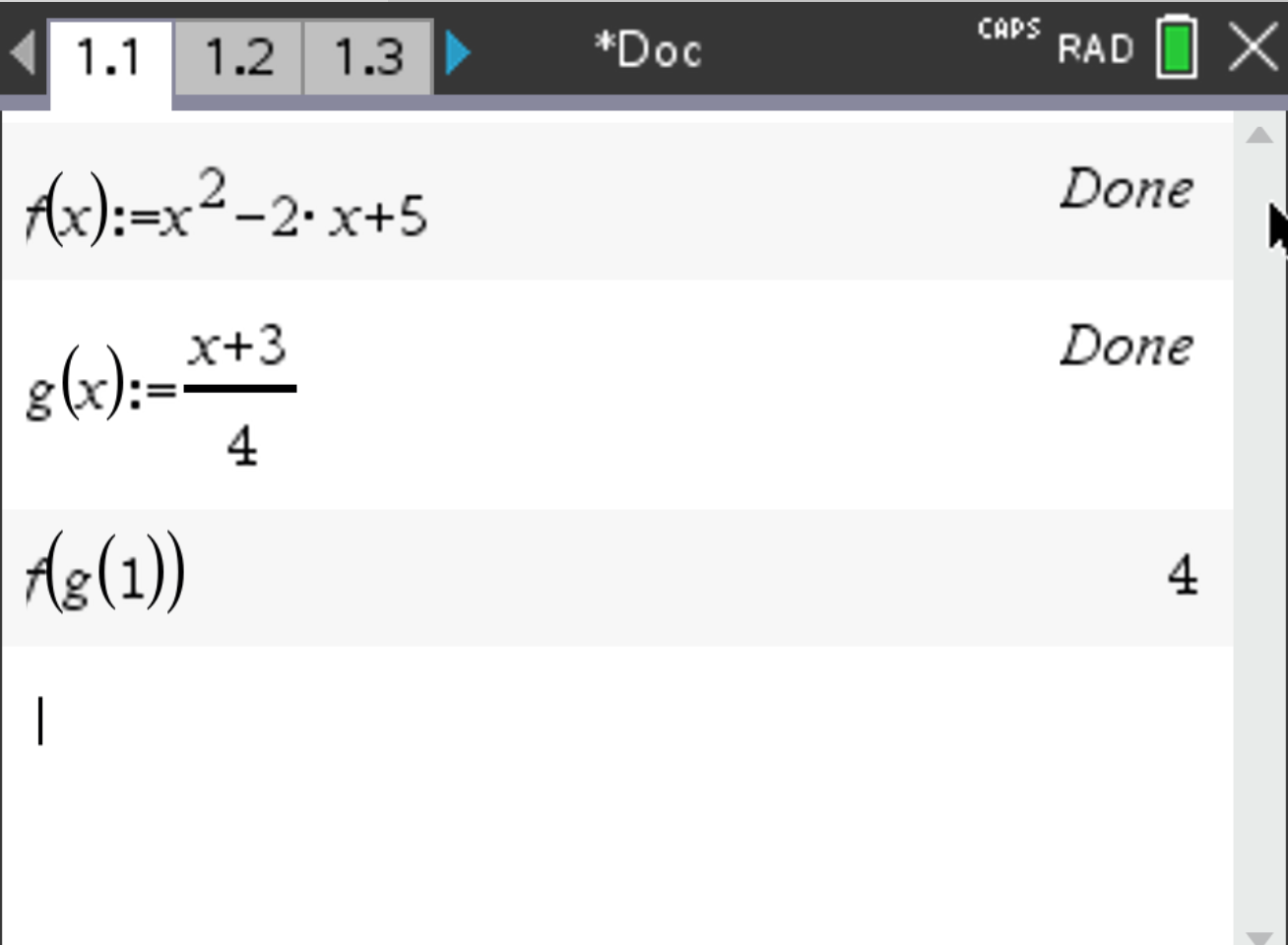
   The result should be \( 4 \). Thus, \( (f \circ g)(1) = 4 \).